[MASM學習筆記]第一課:數字系統與暫存器
在撰寫組合語言之前,必須對數字系統和CPU內部的暫存器有基礎的概念,才有辦法開始撰寫程式。因為組合語言是個十分貼近硬體的低階語言,無法像高階語言一樣能快速的進行記憶體空間的配置,在組語的世界中,需要將使用到的資料大小算得很清楚,否則很容易就讓你吃個OverFlow(溢位)。
數字系統(Numeral System)
數字系統就是表示數字的方法。常用的表示方法有10進制、2進制、8進制和16進制,將在後面一一做介紹。
進制(進位)表示法
所謂進制(進位)表示法,就是在定義一個數在大於等於某數的時候必須進位。好比我們最常用的十進制,當9+1要用數字表示為十的時候,因為9+1已經等於十,必須再往左進位,因此表示為10。如果是八進制要表示十,可以看成7+1+2,7+1等於八,必須要進位,表示為10,最後再加2的話就是12。這樣說其實很模糊,來看看進制的兩個通式。
通式一:一般式
Mr=(anan-1…a2a1a0.a-1a-2…a-m)r
上面公式中,各代數的定義如下:
- M:所要表示的數值。
- r:底數。十進制以10為底;八進制以8為底,依此類推。
- n:最高位的位數。(小數點前從0開始算)
- a:每位數的數值。
- m:小數點後最低位的位數
這是最基本的表示法,若是十進制,數字一百二十三可表示為(123)10或是123(10);若是八進制,數字一百二十三可表示為(173)8或是173(8)。
一個r進制中的各個位數所能接受的數值範圍在0~r-1。
通式二:加權式
Mr=anrn+an-1rn-1+……+a0r0+a-1r-1+……+a-m+1r-m+1+a-mr-m
上面公式中,各代數的定義同上面的通式一。
任何進制皆可藉由加權式將值轉換為十進制。例如有個八進制的數表示為173(8),那麼他的加權式就可以寫成173(8)=1*82+7*81+3*80=64+56+3=123(10)。
常用進制
十進制(Decimal)
十進制為我們最常用的進制系統,日常生活中所見的數字幾乎都是以十進制來表示,例如金錢的數目、年齡、年份、數學。一般來說,未特別指定其進制的數值都會當作是十進制。十進制數值的表示方法如:789、789D、(789)10、789(10)。
二進制(Binary)
在數位的世界中常利用高電位和低電位(沒有電位稱為高阻抗)來當作邏輯訊號。正邏輯1表示高電位,0表示低電位;負邏輯1表示低電位,0表示高電位。在一般情況下我們都是使用正邏輯。由於電子電路中的邏輯只有高電位1和低電位0,故運算方式採用只有1與0的二進制系統。二進制數值的表示方法如:10110B、(10110)2、10110(2)。
八進制(Octal)
為了方便讓程式設計者控制記憶體的內容,可以將二進制數的3個連續的數字合併為1個(例 10110(2)=26(8)),用8進制來表示,才不用輸入一坨拉庫的0與1。八進制數值的表示方法如:567O、(567)8、567(8)。
十六進制(Hexadecimal)
將二進制數的4個連續的數字合併為1個,即為十六進制。十六進制系統可以用在許多地方,除了前面說的可以簡化二進制方便程式設計者控制記憶體的內容外,也可以用於色碼(例如#CFE0EA)。十六進制的每個位數的最大值為十五,但一個阿拉伯數字並沒有「十五」這種數值,故在9之後的數值會以英文字母來代替,例如十會寫成A、十一寫成B、十二寫成C、十三寫成D、十四寫成E、十五寫成F,依此類推。十六進制數值的表示方法如:3A2BH、(3A2B)16、3A2B(16)。如果要利用十六進制來指定某個16位元(2位元組)的記憶體存入1010101010101010B(1、0交錯)的數值,使用二進制來表示會顯得很冗長,而且容易寫錯,這時可以改存入AAAAH(1010(2)=A(16)),會清楚很多,且不易寫錯。
進制換算
為了能在撰寫程式時在適當的時機運用各個進制來表示數值,學會進制的轉換是必須的。
十進制轉任何進制
十進制要轉換成其他進制,整數部份可以利用連除法(可用短除法)來輕鬆達成,小數部份則需使用連乘法。
例題一:68.375轉2進制
首先將整數68做連除法(68為被除數、2為除數)運算,需將餘數寫出來,除到被除數比除數小為止。
68/2=34….0
34/2=17….0
17/2=8….1
8/2=4….0
4/2=2….0
2/2=1….0
此時只要將運算結果倒過來取最後值和所有餘數值即可得到正確的2進制值:68=1000100(2)。
整數取好後再來是小數,將0.375的小數部份做連乘(乘2)計算,直到小數部份為0。
0.375*2=0.75
0. 75*2=1.5
0.5*2=1
此時只要將運算結果按照順序取運算後的整數值即可得到正確的2進制小數值:0.375=0.011(2)。
故68.375=1000100.011(2)。
例題二:75.625轉16進制
首先將整數75做連除法(75為被除數、16為除數)運算,需將餘數寫出來,除到被除數比除數小為止。
75/16=4….11
可知75=4B(16)。
整數取好後再來是小數,將0.625的小數部份做連乘(乘16)計算,直到小數部份為0。
0.625*16=10
可知0.625=0.A(16)。所以75.625=4B.A(16)。
任何進制轉十進制
代入加權式即可轉換。
例題一:1000100.011(2)轉十進制
1000100.011(2) = 1*26 + 0*25 + 0*24 + 0*23 + 1*22 + 0*21 + 0*20 + 0*2-1 + 1*2-2 + 1*2-3 = 64 + 4 + 0.25 + 0.125 = 68.375。
例題二:4B.A(16)轉十進制。
4B.A(16) = 4*161 + 11*160 + 10*16-1 = 64 + 11 + 0.625 = 75.625。
進制的轉換看似很麻煩,多算過幾遍後計算速度自然能加快。這些轉換方法都很基本,事實上還有一些速解法能用,因為不太重要,在此就不介紹了。
進制的加減法
平常我們算數學都是使用十進制來計算,在加法若遇到大於等於10的情況必須要進位;減法若遇到小於0的情況必須要借位。這個規則在其他進制也是一樣,只不過加權值不同罷了。
加法
直接舉個例子來講解:10111(2) + 1001(2)。
從最低位的位數(第0位)開始相加,1+1超過2,因此進位,可以把式子寫成: 10110(2)+ 1000(2) + 10(2)。往左到第1位,1+0+1超過2,因此進位,可以把式子寫成:10100(2) + 1000(2) + 100(2)。第2位,1+0+1超過2,因此進位,可以把式子寫成:10000(2) + 1000(2) + 1000(2)。第3位,0+1+1超過2,因此進位,可以把式子寫成:10000(2) + 10000(2)。第4位,1+1超過2,因此進位,故最後算出來的結果為100000(2)。用直式來計算會比較好表示,如下圖:
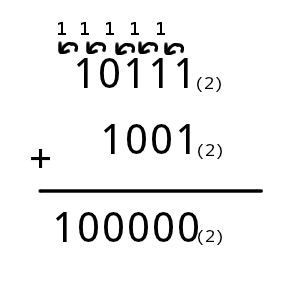
減法
直接舉個例子來講解:10111(2) – 1001(2)。
從最低位的位數(第0位)開始相減,1-1=0,可以把式子寫成:10110(2) – 1000(2)。往左到第1位和第2位均為1-0=1,式子不變。第3位,0-1小於0,因此借位,可以把式子寫成:1110(2) + 1000(2) – 1000(2)。故最後算出來的結果為1110(2)。用直式來計算會比較好表示。
補數
任何r進制均有自己進制本身的r補數與自己進制本身-1的r-1補數,例如一個二進制數擁有2的補數和1的補數,一個十進制數擁有9的補數和10的補數。當然若將十進制數轉換為二進制數,則同樣擁有2的補數和1的補數。
補數觀念最常用於二進制系統,因為這牽涉到有號數及無號數,一般在電腦內表示有號數的方式是使用2的補數,如此才不會有正負零(±0)的問題。
補數也可以用「’s」的方式來表示,例如1的補數可以表示為「1’s」,2的補數可以表示為「2’s」。
補數的轉換方式
在此只談二進制的補數,以10110(2)為例。若要計算1’s,則只要將所有位數填滿為1再減掉原本數值即可,計算方式:11111(2) – 10110(2) = 01001(2)。所以10110(2)的1補數為01001(2)。若要取2補數,只要將1補數再加1即可,如:01001(2) + 1(2) = 01010(2)。
2的補數系統
在上面有稍微提到過電腦內部使用的數值表示法為「2’s」。正負數判斷的依據在於最高位元(Most Significant Bit, MSB)。在有號數的情況下,若MSB為0則為正數,可以直接使用;若MSB為1則為負數,需經過「2’s」轉換後才能使用。在無號數的情況下,MSB不論為0或1均可直接使用。因為有號數的MSB被用來表示數值的正負值,故與無號數所能表示的數值範圍不同。假設有個n位元的數,在有號數的情況下所能表示的數字範圍在-2n-1~2n-1-1,共2n個;在無號數的情況下所能表示的數字範圍在0~2n,共2n個。
以8位元的數字為例,在有號數的情況下所能表示的正數範圍在0~+127(共128個),負數範圍在-1~-128(共128個),合計能表示256個不同的數。若在無號數的情況下所能表示的數字範圍在0~255,同樣能表示256個不同的數。