C++大數乘冪運算！真的是超大數運算！

你有沒有想過，數值資料有沒有上限？不論是什麼型態的數值，均有上限，這是記憶體限制。要如何才能做到超大數運算，就要靠人類聰明的頭腦啦！

以32位元系統來看：

int(整數)型態的數值，範圍是：-2147483648~2147483647 (-2^32-1 ~ 2^32-1 -1)

long long int型態的數值，範圍是：-2^64-1 ~ 2^64-1 -1

就C語言來看，long long int已經是最大的整數型態了！

我們就姑且先用「long long int」來寫一個大數乘冪運算程式吧！

寫一個C++程式，讓使用者輸入兩個整數(n,m)，並且計算n^m的值和值的位數

乘冪運算(一般)

在先前的教學中，我們提到乘冪運算函數「pow」，但它有先天的限制不能用在大數運算，那就是pow出來的值，一定要用浮點數儲存(float、double)。使用浮點數，就不能進行大數運算了！

我們現在要寫的程式，就是不用pow，也能有相同的乘冪效果，要如何做到呢？

使用for迴圈，可以計算底數要乘的次數，如此一來就可以做乘冪運算了。

方法如下：

power=1; //power為乘冪運算後的結果

for(i=1;i<=m;i++) //i為for計次變數

power*=n;

乘冪運算式寫出來了，再來就寫位數取得程式吧！

如何取得位數呢？在日常生活中，「7777」我們一看就知道這是4位數，「98234」一看就知道是5位數，這是為什麼呢？因為我們可以直接從這串數字中，快速地算出這串數字有幾個數字。電腦如果想要做到這種方法的話，想必就得靠除法了。以「5566789」為例，「5566789」是一個大於零的數，因此我們可以判斷它一定至少有一個位數。接著，我們可以將其除以10，小數點後自動捨去，可以再判斷它是否還大於零，如果是，那我們可以判斷它至少有兩個位數。依此類推，可推得「5566789」是7位數。將上面方法轉換成程式碼如下：

s=0; //s用來記錄整數位數

while(power>=1) //取得整數位數
{
power=power/10; //去掉最後一位
s++; //位數加一
}

綜合上面方法，我們可撰寫出程式了，程式碼如下：

#include<iostream>
using namespace std;
 
int main()
{
    long long int n,m,power; //n是底數；m是指數；power是乘冪運算結果
    int s,i; //s用來計算整數位數；i是for的計次變數
    while(true)
    {
        s=0;
        power=1;
        cout << "請輸入二整數n,m，本程式將計算n^m: ";
        cin >> n >> m;
        for(i=1;i<=m;i++) //乘冪運算迴圈
            power*=n;
        cout << "值：" <<  power; //先輸出運算結果
        while(power>=1) //取得整數位數
        {
            power=power/10; //去掉最後一位
            s++; //位數加一
        }
        cout << endl << "共" << s << "個位數" << endl;
    }
    return 0;
}

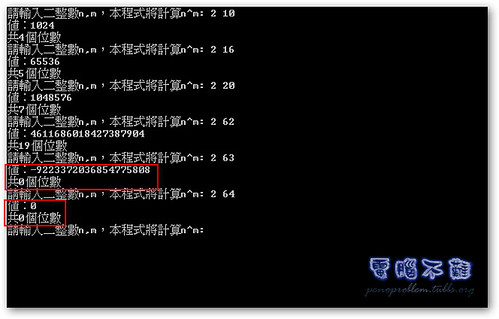
從上圖可知，使用long long int 最多也只能算到2⁶³，如何做出真正的超大數運算，還有待思考

大數乘冪運算(慢)

long long int最多也只能存到2⁶³-1，要如何才能超過這個範圍呢？當你要將一個好幾GB的檔案燒到CD光碟裡，你會怎麼做？正常人應該都會「分割」檔案。同理，我們也可以將數據分開存到變數之中。最簡單的方法，就是使用陣列，將每一個數字分別存到不同的int陣列中。舉個例子，「1234」我們須將它分開存入x陣列中，即x[0]=4,x[1]=3,x[2]=2,x[3]=1，輸出只要倒過來輸出即可。

由於這個部分比較複雜，所以先附上程式碼，再做講解，程式碼如下：

#include<iostream>
using namespace std;
 
int main()
{
    int a,i,b; //a是計次變數(指數的)；i是第幾位數之變數；b是計次變數(輸出的)
    int n,m,v,s; //n是底數；m是指數；v是進位暫存變數；s用來記錄整數位數
    while(true)
    {
        cout << "請輸入二整數n,m，本程式將計算n^m: ";
        cin >> n >> m;
        int x[500000]={0}; //宣告int x陣列
        v=0; //清空v的值
        s=1; //不管怎麼樣，s必會大於等於1，因為整數一定有位數
        x[0]=1; //先讓最早要乘的這格陣列值等於1
        for(a=1;a<=m;a++)
        {
            for(i=0;i<s;i++)
            {
                x[i]=x[i]*n+v; //各個位數運算式，v是有進位時要加上去的
                v=x[i]/10; //v若大於0，則需進位
                x[i]=x[i]%10; //每格陣列存一位數
                if(v!=0&&i+1==s) //判斷位數是否+1
                s++; //記錄整數位數
            }
        }
        cout << "值：" ;
        for(b=s-1;b>=0;b--) //反向輸出
            cout << x[b];
 
        cout << endl;
        cout << "共" << s << "個位數" << endl;
    }
 
    return 0;
}

以底數2舉例

2的值，表格如下(點圖放大)：

分解表格(點圖放大)：

用文字說明實在會很冗長，不是很好理解，所以我就製作了表格給各位。不過我還是說一下好了，假設我要計算到2²⁰，我們會先從2¹、2²、2³……一直算到2²⁰，文字分解如下：

n=2、m=20、x[0]=1、s=0、v=0。首先進入for迴圈，a=1、i=0，x[i]=x[0]=x[0]*n+v=1*2+0=2，v=x[i]/10=x[0]/10=2/10=0，x[i]=x[i]%10=x[0]%10=2%10=2，因為v為0，所以不執行if敘述。故2¹為2。

第二次執行for迴圈，a=2、i=0，x[i]=x[0]=x[0]*n+v=2*2+0=4，v=x[i]/10=x[0]/10=4/10=0，x[i]=x[i]%10=x[0]%10=4%10=4，因為v為0，所以不執行if敘述。故2²為4。

第三次執行for迴圈，a=3、i=0，x[i]=x[0]=x[0]*n+v=4*2+0=8，v=x[i]/10=x[0]/10=8/10=0，x[i]=x[i]%10=x[0]%10=8%10=8，因為v為0，所以不執行if敘述。故2³為8。

第四次執行for迴圈，a=4、i=0，x[i]=x[0]=x[0]*n+v=8*2+0=16，v=x[i]/10=x[0]/10=16/10=1，x[i]=x[i]%10=x[0]%10=16%10=6，因為v為1，i+1=0+1=1=s，所以執行if敘述，s=s+1=2。再次執行for迴圈(i)，i=1，x[i]=x[1]=x[1]*n+v=0*2+1=1，v=x[i]/10=x[1]/10=1/10=0，x[i]=x[i]%10=x[1]%10=1%10=1，因為v為0，所以不執行if敘述。故2⁴為16。

第五次執行for迴圈，a=5、i=0，x[i]=x[0]=x[0]*n+v=6*2+0=12，v=x[i]/10=x[0] /10=12/10=1，x[i]=x[i]%10=x[0]%10=12%10=2，因為v為1，i+1=0+1=1不等於s(=2)，所以不執行if。第二次執行for迴圈(i)，i=1，x[i]=x[1]=x[1]*n+v=1*2+1=3，v=x[i]/10=x[1]/10=3/10=0，x[i]=x[i]%10=x[1]%10=3%10=3，因為v為0，所以不執行if敘述。故2⁵為32。

依此類推，一直到第二十次執行for迴圈，a=20、i=0、s=6、v=0，x[i]=x[0]=x[0]*n+v=8*2+0=16，v=x[i]/10=x[0] /10=16/10=1，x[i]=x[i]%10=x[0]%10=16%10=6，因為v為1，i+1=0+1=1不等於s(=6)，所以不執行if。

第二次執行for迴圈(i)，i=1，x[i]=x[1]=x[1]*n+v=8*2+1=17，v=x[i]/10=x[1]/10=17/10=1，x[i]=x[i]%10=x[1]%10=17%10=7，因為v為1，i+1=1+1=2不等於s(=6)，所以不執行if。

第三次執行for迴圈(i)，i=2，x[i]=x[2]=x[2]*n+v=2*2+1=5，v=x[i]/10=x[2]/10=5/10=0，x[i]=x[i]%10=x[2]%10=5%10=5，因為v為0，所以不執行if敘述。

第四次執行for迴圈(i)，i=3，x[i]=x[3]=x[3]*n+v=4*2+0=8，v=x[i]/10=x[3]/10=8/10=0，x[i]=x[i]%10=x[3]%10=8%10=8，因為v為0，所以不執行if敘述。

第五次執行for迴圈(i)，i=4，x[i]=x[4]=x[4]*n+v=2*2+0=4，v=x[i]/10=x[4]/10=4/10=0，x[i]=x[i]%10=x[4]%10=4%10=4，因為v為0，所以不執行if敘述。

第六次執行for迴圈(i)，i=5，x[i]=x[5]=x[5]*n+v=5*2+0=10，v=x[i]/10=x[5]/10=10/10=1，x[i]=x[i]%10=x[5]%10=10%10=0，因為v為1，i+1=5+1=6等於s(=6)，所以執行if敘述，s=s+1=7。

第七次執行for迴圈(i)，i=6，x[i]=x[6]=x[6]*n+v=0*2+1=1，v=x[i]/10=x[6]/10=1/10=0，x[i]=x[i]%10=x[6]%10=1%10=1，因為v為0，所以不執行if敘述。故2²⁰為1048576。

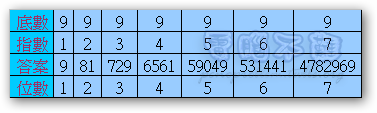
以底數9舉例

9的值，表格如下(點圖放大)：

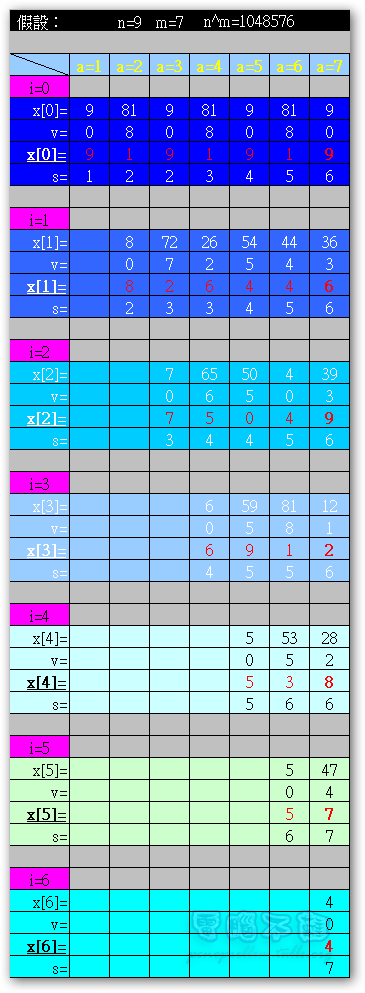
分解表格(點圖放大)：

原理同上，我就不再說明了

使用此種方法寫出來的程式，可以計算到500000位數，因為500000格陣列，每格存一個數字。這種方法雖然簡單，可是卻是一種很緩慢的算法，畢竟，int可以存到10個位數，可是我們卻只讓它存1個數字，所以這其實是很浪費資源的。

大數乘冪運算(快)

如果我們讓每格陣列中，多儲存一些數字，想必能加快運算速度。其程式碼如下：

#include<iostream>
#include<iomanip>
using namespace std;
 
int main()
{
long int a,i,b,d; //a是計次變數(指數的)；i是第幾位數之變數；b是計次變數(輸出的)；d是位數-1，即陣列的最大值
long long int n,m,v,s; //n是底數；m是指數；v是進位暫存變數；s用來記錄整數位數
while(true)
{
cout << "請輸入二整數n,m，本程式將計算n^m: ";
cin >> n >> m;
long long int x[100000]={0}; //宣告int x陣列
v=0; //清空v的值
s=1; //不管怎麼樣，s必會大於等於1，因為整數一定有位數
x[0]=1; //先讓最早要乘的這格陣列值等於1
for(a=1;a<=m;a++)
{
for(i=0;i<s;i++)
{
x[i]=x[i]*n+v; //各個位數運算式，v是有進位時要加上去的
v=x[i]/1000000000; //v若大於0，則需進位
x[i]=x[i]%1000000000; //每格陣列存九位數
if(v!=0&&i+1==s) //判斷陣列是否+1
s++; //記錄陣列位數
}
}
 
cout << "值：" ;
for(b=s-1;b>=0;b--) //反向輸出
{
if(b!=s-1) //最前面的陣列前面不能補0
cout << setfill('0') << setw(9) << x[b];
else //最前面的陣列輸出
cout << x[b];
}
cout << endl; //換行
 
if(i==1) //如果整數不超過一個陣列(即不超過9位數)
{
s=0; //陣列位數清除
while(x[0]>=1) //取得整數位數
{
x[0]=x[0]/10;  //去掉最後一位
s++;  //整數位數加一
}
}
else //如果整數超過一個陣列(即超過9位數)
{
d=s-1; //d是陣列最大值
s=(s-1)*9; //陣列位數扣掉最前面的陣列再乘9，就是扣掉最前面的陣列目前的整數位數
while(x[d]>=1) //取得整數位數
{
x[d]=x[d]/10; //去掉最後一位
s++; //整數位數加一
}
}
 
 
cout << "共" << s << "個位數" << endl;
}
 
return 0;
}

瞭解並完成程式後，計算99⁹⁹、999⁹⁹和9999⁹⁹再也不困難！
這個程式可以算到100000*9位的整數，算很多了呢！如果還嫌不夠，自己再加開陣列吧！

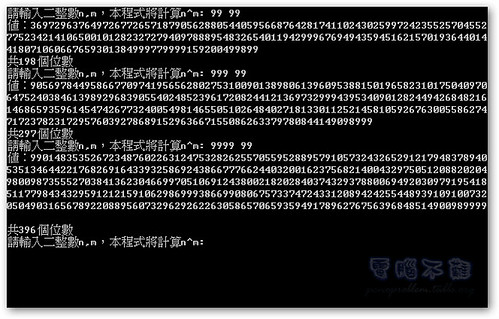
就連9999¹⁰⁰⁰⁰也能夠快速算出！

大數運算可是很好玩又很有挑戰性的呢！！

電腦不難