快速排序法(Quick sort)

快速排序法算是比較進階的排序方法，它的速度在大多數的情況下比前面四種都快，當然也難了許多。大致上來說，就是先在陣列中找出一個Pivot(支點)點，在此都用最左邊，作為數字比大小的基準。然後從陣列的左邊和右邊，建立出一個能活動指標，分別往右和往左搜尋比Pivot大或比Pivot小的值，之後再將搜尋到的值交換。若兩方向的活動指標並未搜尋到適當的值(判斷方法為向右指標>=向左指標)，則將Pivot值與向左搜尋的活動指標所指的索引位置調換，切成左右兩邊再搜尋一次。

圖解快速排序法

假設現在有個陣列：[69,81,30,38,9,2,47,61,32,79] 要如何將它遞增排列呢？

首先設[索引0]為pivot點(粗體表示)，接著建立兩個指標分別從[索引1]和[索引9]開始向右和向左搜尋數值。一開始向右指標(紅點)就找到比pivot值還要大的數，因此停下來。而向左指標(藍點)則繼續向左搜尋。

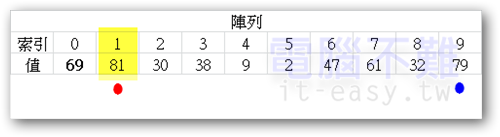
直到紅點和藍點兩方都各自找到比pivot大的數和比pivot小的數，且紅點在藍點的左邊，則交換這兩個數。

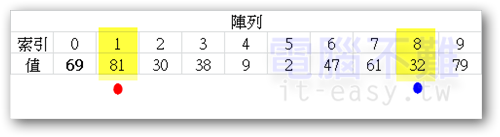
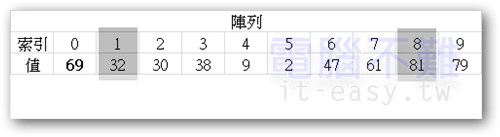
繼續維持同樣的方向搜尋。此時藍點又找到比pivot小的數而停下來。

可當紅點找到比pivot大的數時已經為時已晚。當紅點跑到藍點右邊時，藍點所指到的值必須跟pivot值交換。

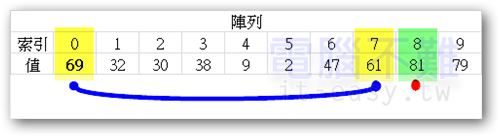
交換後，pivot值變為61，依然在[索引0]上。藍點所指的索引位置不變，但紅點得重新計數。

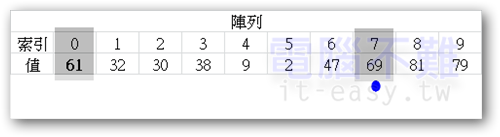
pivot改變後，繼續搜尋。很快的藍點又找到了比pivot小的數。

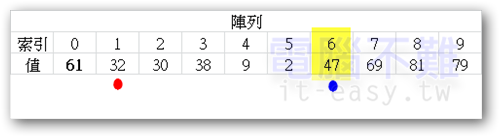
當紅點終於找到pivot大的數時，又不幸的跑到藍點的右邊了。所以pivot的值要再換一次。

有沒有發現[索引0]的值在不知不覺中變小了！？

繼續搜尋，藍點又找到比pivot還更小的值了。

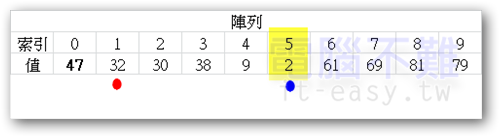
再換一次pivot。

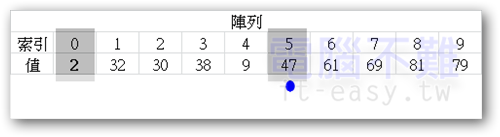
從上圖可知pivot點，也就是[索引0]的位置目前存放著陣列的最小值。想當然，紅點隨便找都有比pivot大的數；藍點怎麼找都找不到比pivot小的數。

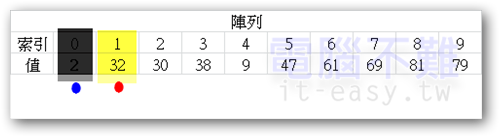
當藍點不幸移動到pivot點的位置，則pivot要往右移一格。原先的pivot點，也就是[索引0]的值就固定不變了。無論是紅點或是藍點都無法觸及。現在的pivot值為32，紅藍點要回到起點重新出發。(紅點起點在pivot的右邊一格；藍點起點在陣列的最右邊)

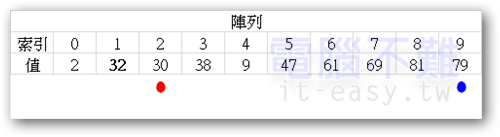
經過搜尋後，紅、藍點都各自找到了自己的歸屬，且紅點在藍點的左邊。所以他們所指的索引元素值得互相交換。

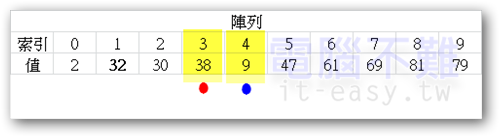
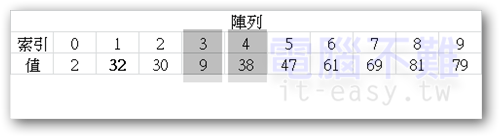
此時紅點往右一格，藍點往左一格，又會碰上紅點在藍點右邊的狀況。pivot值又要改變了！

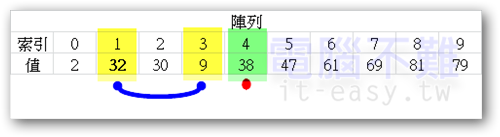
藍點繼續從原位向左搜尋，而紅點則回到起點(pivot的右邊一格)。最後藍點又會跑到pivot上。所以pivot要左移。

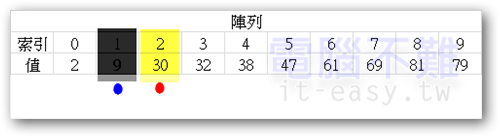
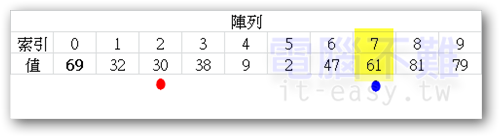
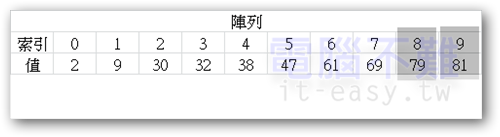
從上圖來看，我們可以發現在不知不覺中[索引0~7]都已經遞增排好了，剩下沒排的就是[索引8、9]。將pivot點跳到[索引8]，再搜尋一次，紅點又跑到藍點右邊。故[索引8]的值要跟藍點所在的[索引9]值調換。

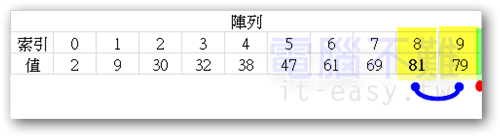
如此一來整個陣列都是以遞增的方式來排列啦！

快速排序法程式碼

	public static int[] exchange_sort(int[] ori_arr, boolean isIncrease){ //交換排序（Exchange sort）
		int[] arr=ori_arr.clone(); //將arr陣列位址指向新複製出來的ori_arr陣列。確保原始陣列資料不會改變。
		int len=arr.length; //取得陣列長度
		for(int i=0;i<len-1;i++){
			for(int k=i+1;k<len;k++){
				if((isIncrease&&arr[i]>arr[k])||(!isIncrease&&arr[i]<arr[k])){ //遞增遞減判斷
						int buffer=arr[i];
						arr[i]=arr[k];
						arr[k]=buffer;
				}
			}
		}
		return arr;
	}